セミナーの主題:4次元の数理科学
日時:8月25日(火)13:00-17:00
場所:東洋大学川越キャンパス1号館2階1204室
(アクセス http://www.toyo.ac.jp/site/access/access-kawagoe.html)
プログラム:
13:00-13:15 吉野隆 「4次元の数理と放散虫骨格構造の関係」
13:15-14:15 海野啓明「4次元折り紙と4次元正多胞体の皮むき展開図について」
14:15-15:15 松浦昭洋「四次元空間の可視化手法とツール」
15:30-16:30 小紫誠子「4次元超立方体内を流れる4次元流体の数値シミュレーション」
16:30-17:00 吉野隆 「4次元のキューブパズル」
要旨:
○海野啓明「4次元折り紙と4次元正多胞体の皮むき展開図について」
4次元折り紙の例として,正4面体の折りたたみを考える.稜角二等分折りと平坦に折りたためるが,体積一定の条件では連続的には折れない.次に,4次元正多胞体の特徴とそのリンゴの皮むき展開図(3次元のS字形螺旋)について紹介する.
○松浦昭洋「四次元空間の可視化手法とツール」
本講演では、部分空間への射影の並列表示や部分空間間の効果的な遷移法を利用した四次元空間可視化ツールを紹介する。また、二つの二次曲線間に一般に四つ存在する複素交点を四次元空間で可視化するツールも紹介する。
○小紫誠子「4次元超立方体内を流れる4次元流体の数値シミュレーション」
4次元非圧縮ナビエ・ストークス方程式を用いて4次元超立方体内部を流れる流れの数値シミュレーションを行う.現実の3次元流れの解析において,4次元流れとの流体構造との違いから流れの本質を探るアプローチが考えられる.本講演では,まず4次元流れを捉える可視化についての試みを紹介する.
○吉野隆「4次元のキューブパズル」
一辺が三分割された立方体の表面の色を揃える「あの立体パズル」の4次元版について検討する.パズルを構成するパーツ,パーツの回転,パズルの可視化,パズルのインターフェイスなどについて現状を紹介する.
○吉野隆「4次元の数理と放散虫骨格構造の関係」
本研究会の目的と意義を述べる.
Saturday, January 10, 2015
なので,Tweet-a-Program への投稿はやっておりません.やりたい気持ちもあるけど,Tweet-a-Program は常に動いているわけじゃなさそうでロスが多いんです.「せっかく送ったのに無視」っていうケースが何度もありました.もう少し向こうもこちらも安定したら再開しようと思います.
Thursday, November 13, 2014
こんな感じです.たまに日付が飛んでいるのは先方がダウンしていたためです.
[2014/11/02]
[2014/11/03]
[2014/11/04]
[2014/11/05]
[2014/11/06]
[2014/11/07]
[2014/11/08]
[2014/11/09]
[2014/11/11]
Tweet-a-Program 氏(@wolframtap)に Mention で Mathematica のコード(Wolfram言語のプログラム?)をつぶやくと計算結果の画像を RT してくれるというシステムで遊んでみることにしました.ネタが続く限りつぶやき続けようと思います.昨日はライフゲーム(Game of Life)のグライダーを今日はオフラティスのランダムウォークをつぶやきました.暇があれば解説を書こうと思います.たぶん,書かないと思うけど….
前からほしかった孔明鎖と呼ばれているおもちゃです.やっと Amazon のマーケットプレイスで発見しました.中国から直接送られてきたらしいです.箱を開けたとたんに揮発性薬品の臭いがしたのが少し心配ですが….
These toys were played in ancient China. They were said to be invented by Zhuge Liang.

I prepared the Mathematica files and CVS files which included the basic data of 4D polytopes. The zipped file contains 6 files which correspond to 6 regular polytopes: 5 cells, 8 cells, 16 cells, 24 cells, 120 cells, and 600cells. Each file consists of 6 basic properties as follows:
- Locations of vertices of the polytope
- Pairs of vertex numbers which consists edges of the polytope
- Vertex numbers of adjacent vertices of each vertex of the polytope
- Vertex numbers of each face of the polytope
- Face numbers of adjacent faces of each face of the polytope
- Face numbers of each cell of the polytope
Unzipped filenames are like “f (n). m” where (n) corresponds to the number of cells. For 5 cells, its filename is “f5.m” for example. If we assume that these files allocated on the directory “~/tmp/”, we can use the data like the following:
With[{n = 24, dir = “~/tmp/”},
Module[{vers, edgs, neis, faces, fneis, cells},
{vers, edgs, neis, faces, fneis, cells} =
Get[dir <> “f” <> ToString[n] <> “.m”];
cells
]
]
Please inform me if you find any mistake.
- Data (Mathematica, zip)
- Data (csv, zip)
- Notebook (in preparation)
- PDF (in preparation)
4次元正多胞体の基本データをまとめた Mathematica のファイルおよび CSV ファイルを公開します.6種類の正多胞体(5, 8, 16, 24, 120, 600)について,以下の6種類のデータが保存されています.
- 頂点の位置:4次元ベクトルを頂点数だけ並べたもの.
- 辺をつくる頂点の対:1対(つまり2個)の頂点番号を辺の数だけ並べたもの.
- それぞれの頂点に隣接する頂点の番号:隣接する頂点番号のリストを頂点の数だけ並べたもの.
- 面をつくる頂点の番号:面を構成する頂点の頂点番号のリストを面の数だけ並べたもの.
- 隣接する面の番号:隣接する面の面番号リストを面の数だけ並べたもの.
- 胞を作る面の番号:胞を作る面の面番号リストを胞の数だけ並べたもの.
データは多胞体ごとに別のファイルです.正n胞体についてのデータは “f(n).m” というファイル名になります.(n) には数字が入ります.例えば,正5胞体ならデータファイルは “f5.m” ですし,正120胞体ならデータファイルは “f120.m” です.このファイルが “~/tmp/” というフォルダにあるとき,以下のように使用することができます.例えば,「正24胞体を作る24個の胞(立体)が何番目の多角形を用いて作られているのか」は以下のようにして得られます.
With[{n = 24, dir = “~/tmp/”},
Module[{vers, edgs, neis, faces, fneis, cells},
{vers, edgs, neis, faces, fneis, cells} =
Get[dir <> “f” <> ToString[n] <> “.m”];
cells
]
]
より具体的な例はノートブックかPDFファイルを見て下さい.すべての番号は1から始まっているので C 言語などの配列が0から始まる言語で使用する場合にはすべての番号を1だけ少なくする処理が必要です.おそらく他にあまり例がないと思うので公開することにしました.誤りがあったらご指摘願います.
- データ(Mathematica, zip)
- データ(csv, zip)
- ノートブック
- PDF
2014/06/13 に迷路の話を 06/15 に WORLDEYE の話を第77回形の科学シンポジウムで発表してきました(前者は講演,後者は展示).どちらの話もこれで終わりになるかな?
迷路の話についてはいろいろ考えたけど,現在の私の立場は「粘菌の探索をもとにしたアルゴリズムを模索することには意義があるが,知性の有無についてはそれほど重要なこととは思えない」という感じです.粘菌の知性について論じること自体は「石を投げる」という意味で価値があるとは思います.
WORLDEYE については,開発者がもっと情報公開を行うべきだと考えています.できれば私はもっと高解像度な高精度な全球面版がほしい.
発表用に作成した新しい画像を添付します.説明は省略します.

Wednesday, January 29, 2014
迷路の中は流体で満たされていて,初期状態でその圧力は0としましょう.赤で示した入口の圧力を常に100に,出口の圧力を常に0にして,入口と出口の圧力差が常に 100になるようにします.そして,圧力についてのラプラス方程式の数値解を求めます.左の図がその結果を図示したものです.圧力100が白,圧力0が黒で,グレースケールで迷路内の圧力分布を表示しています.右の図は隣のマスとの差の(圧力勾配)絶対値の最大値を表しています.差の絶対値が最も大きいところが白,差がゼロであるところを黒として,グレースケールで圧力勾配の分布を示しています.圧力勾配は流体の流れる方向に相当しています.右の図は迷路の解をたどって流体が流れていることを示しています.つまり,流体は迷路の答えを得たことになります.Mathematica で2時間ぐらいコーディングしたらできちゃいました.夏ぐらいからやろうと思っていたものでした.早くやればいいのに,ダラダラしちゃって….
周囲の情報で全体が変わっていく.創発ってこんな感じのことなのではないかと思っています(違うのかな?)
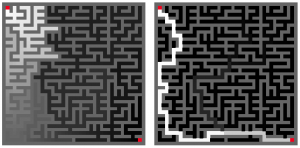
Fluid flow in maze.
.
球面上のパターン形成をプレゼンテーションするのにピッタリなおもちゃ「学研ワールドアイ」(学研ワールドアイのページ)を入手しました.同梱された USB メモリに入っているデータだけではなく,自分で作ったデータも表示できるようです.
I got a toy “World Eye” which is useful for presentations of pattern formation on spherical surface. This toy can project the data made by users.
そこで,自分でもデータを作ってみようと思いました.しかし,わかっていることは少なくて,画像サイズは640×480で実際には中央の480×480に内接する円内部の画像のみが投影されることぐらいです.そこで,自分で試してみることにしました.
So I tried to construct my data and project them using this toy. But information is few.

ステレオ投影の理論は単純です.ウィキペディアに解説があります(ウィキペディア「ステレオ投影」).私はz軸を逆に取っているので,(x, y) を 1/(1+z) 倍した図形を作って,うまく映るのかを確かめてみました.
At first, I transformed (x, y, z) to (x/(1+z), y/(1+z)) where z is greater than zero and examined the projection.

ご覧のとおり,緯線の曲がり方がきつすぎるようです.視点はもっと奥にあるようです.
As shown in the image, the latitude curves were incorrect.
そこで,視点を 1 だけ奥にしてみました.視点が a だけ奥に行くと変換は (1+a)/(1+a+z) 倍になります.今回は 2/(2+z) 倍です.確かめてみると,そこそこ良いようです.しばらくは,視点が中心から直径分だけ奥にあると仮定して画像を作ろうと思います.
I change the view point from 1 to 2. In such case, the point (x, y, z) is transformed to (2 x/(2+z), 2 y/(2+z)). The examination is good.

そんなわけで,アニメーションも作ってみました.(アニメーションを撮影したビデオ.数秒でおしまいになります).
次は Turing pattern を表示してみたいと思っています.いつになるかわからないけど.






